ある日の1~3年生クラスでのことです。私が思考力教材「なぞぺー」で、平面図形問題の解説をしていました。
「同じ大きさ、同じ形で敷きつめるんだよ」という主旨を伝えてからこう言いました。「2~3年生になると、こんなふうにレベルアップします。おおもとの形すら与えられていません。わかっているのはいくつ入るかだけ。」
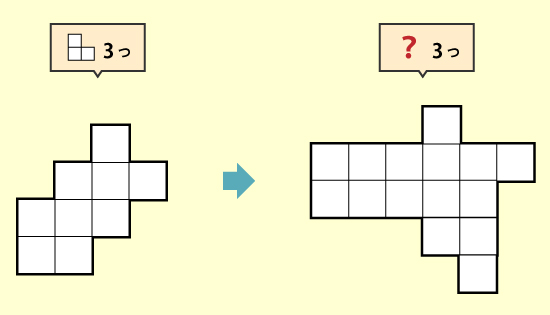
その瞬間、返ってきたのは「ぃよっしゃあ~!!」という2年生の声。見ると、その発言をした子ばかりでなく、周りの子も「そうこなくっちゃ!」というキラッとした目をこちらに向けています。そう、なぞぺーで養いたいのは、この“考えること自体へのポジティブさ”なのです。
なぞぺーの目的は、「子ども自らがわかった!と思える成功体験=わかっちゃった体験を積むことで、自ら取り組む主体性、意欲を育てる」これに尽きます。意欲が養われてこそ、様々な分野の問題に継続して触れ、思考のセンスを磨いていくことができます。
知識が十分になくても意欲があれば、入試問題も考えられるかもしれません。これは低学年でも楽しめそうだぞ!と思うものがありました。
2018年度の麻布中学校の算数です。
2つの記号○、×を並べてできる列のうち、次の条件にあてはまるものを考えます。
(条件)○が3つ以上連続して並ぶことはない。
例えば、○○×○○はこの条件に当てはまりますが、○×○○○××は条件にあてはまりません。
問1)○、×を合わせて14個並べるとき、×の個数が最も少なくなる列を1つ書きなさい。
問2)○、×を合わせて13個並べるとき、×の数が最も少なくなる列は全部で何通り考えられますか。
問3)○、×を合わせて12個並べるとき、×の個数が最も少なくなる列は全部で何通り考えられますか。
問3は場合分けが必要な問題です(花まるでは場合分けという言葉は4年生以降に発展版Sなぞぺーで学びます。しかし、実は低学年なぞぺーでもそういった問題を扱っています)。ただ問1や問2は、手を動かして書きだすことを通じて、ある“決まり”を見いだせればあっという間に解けます。
問1)○○×○○×○○×○○×○○
問2)問1を通じて、「3個に1個は必ず×がある」ということに気づけたでしょうか。今度は13個ですから、×は必ず4個あります。
○○×○○×○○×○○×○
右端にある「○」は、他の4つの「○○」と入れ替え可能です。したがって答えは5通りです。
大事なことなので再度書きますが、「できるかどうか」ではなく「楽しめるか」そして「つまずきすら含めておもしろがれるか」これが、なぞぺーなどの思考力問題を通じて最終的に体現したい学習者像です。
「考える」ということには、実は「つまずき」が織り込まれています。「あれ?」「おや?」「どういうこと?」「何が問われている?」「うーんここまではわかる」…つまずきがなければ、考えるということ自体が成立しません。
考えた結果→正解になった。そんなことが常に起こるのは「答えとセットになってあらかじめ用意されている問題」においてだけです。社会に出たらプロセスだらけ。答えは自ら定義し、検討修正し、時に周囲とすり合わせていくものです。だからこそ、正解不正解ではない、考える=つまずく過程それ自体に価値があるんだ、おもしろいんだと体感した経験や回数を、たっぷり積ませ、認めたいと考えています。
子どもたちの、考えることに没頭している表情が、私は大好きです。「わかっちゃった!」の前に「わかった」の瞬間があり、それは笑顔ではなく、惚(ほう)けたような表情なんですよ。
さあ今日も、たくさんの「わかっちゃった!」を生み出します。
花まる学習会 竹谷和
*・*・*花まる教室長コラム*・*・*
それぞれの教室長が、子どもたちとの日々のかかわりのなかでの気づきや思いをまとめたものです。毎月末に発行している花まるだよりとともに、会員の皆様にお渡ししています。






